A Scatter Diagram provides relationship between 2 variables, and provides a visual correlation coefficient.

Why You Would Use Scatter Analysis and Besprinkle Plots

A Scatter Analysis is used when you need to compare 2 data sets against each other to see if there is a relationship. Besprinkle plots are a way of visualizing the relationship; past plotting the data points you lot get a scattering of points on a graph. The analysis comes in when trying to discern what kind of pattern – if any – is present. And what that pattern means.

It is this kind of assay we are talking about when we are trying to get at the root cause of an issue.

Scatter Diagrams are used to show the "cause-and-issue" relationship between two kinds of information, and to provide more useful information well-nigh a production process.

Specific instances of when to utilize scatter diagrams:

  • Pairs of numerical figures are present
  • Dependent variables have multiple values for each effigy associated with the independent variable
  • Defining if there is a relationship between two variables

What Kind of Data Should You Use on Scatter Analysis?

Besprinkle analysis generally makes employ of continuous data. (See notes on the different data types here.)

Discrete data is best at laissez passer/ fail measurements. Continuous information lets y'all measure things deeply on an space set and is by and large used in scatter analysis.

You could use discrete data on ane centrality of a scatter plot and continuous data on the other axis. For the discrete data, you'd have to put it into some kind of quantified band – like say one-10 on a customer satisfaction score.

I suppose y'all also *could* put detached data that comes out like pass/fail as one of 2 bands, only it would really depend on the data if you got whatsoever useful data out of information technology.

Best bet is continuous data.

If you are looking for a way to do graphical analysis on discrete data, you might try attribute charts.

Besprinkle Plot Videos

Scatter Plots and Correlation

Scatter plots only prove correlation. They do not prove causation. The example often used is shark attacks and ice cream sales. There may exist a correlation between the ii, only ice cream does not cause shark attacks — the heat of the mean solar day does. In other words, more people are in the water on hot days equaling more shark attacks, and more people buy water ice cream on hot days

How to Make a Scatter Diagram:

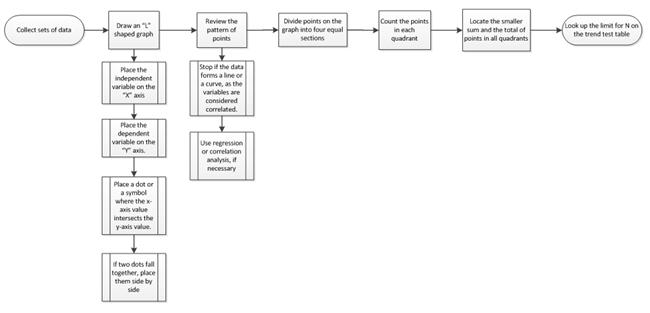
how to make a scatter plot
  1. Collect sets of data where a relationship is present.
  2. Depict a graph in the shape of an "L," and brand the scale fifty-fifty multiples (i.eastward., 10, 20).
    • Place the independent variable on the horizontal (X) axis.
    • Place the dependent variable on the vertical (Y) axis.
    • Identify a dot or a symbol where the x-axis value intersects the y-centrality value.
    • If 2 dots fall together, place them side past side, so they are touching, and both are visible.
  3. Review the pattern of points to determine if a human relationship is present:
    • Stop if the information forms a line or a curve, as the variables are considered correlated.
    • Use regression or correlation analysis, if necessary. If regression or correlation analysis are non needed, complete steps four through vii below.
  4. Separate points on the graph into four equal sections. If X points are present on the graph:
    • Count X/2 points from top to bottom and describe a horizontal line.
    • Count 10/2 points from left to right and draw a vertical line.
    • If the number of points is odd, draw a line through the heart indicate.
  5. Count the points in each quadrant.

Notation: Do not count points on a line.

  1. Locate the smaller sum and the total of points in all quadrants, and add together the diagonally reverse quadrants:

A = points in upper left + points in lower right

B = points in upper right + points in lower left

Q = the smaller of A and B

North = A + B

  1. Expect up the limit for Due north on the trend test table:
  • If Q is less than the limit, the 2 variables are related.
  • If Q is greater than or equal to the limit, the design may have originated from random chance.