How To Find Inverse Of A Square Root Function
3.8: Inverses and Radical Functions
- Folio ID
- 1350
Learning Objectives
In this department, you will:
- Find the inverse of an invertible polynomial function.
- Restrict the domain to find the inverse of a polynomial part.
A mound of gravel is in the shape of a cone with the tiptop equal to twice the radius.
The volume is institute using a formula from uncomplicated geometry.
\[ \begin{align*} V&=\dfrac{one}{3}\pi r^2h \\[4pt] &=\dfrac{1}{3}\pi r^2(2r)\\[4pt] &=\dfrac{ii}{iii}\pi r^3 \end{align*}\]
We have written the volume \(Five\) in terms of the radius \(r\). However, in some cases, we may get-go out with the book and desire to detect the radius. For case: A client purchases 100 cubic feet of gravel to construct a cone shape mound with a height twice the radius. What are the radius and height of the new cone? To answer this question, nosotros use the formula
\[r=\sqrt[3]{\dfrac{3V}{2\pi}} \nonumber\]
This office is the changed of the formula for \(V\) in terms of \(r\).
In this section, we will explore the inverses of polynomial and rational functions and in particular the radical functions nosotros encounter in the procedure.
Finding the Inverse of a Polynomial Function
Two functions \(f\) and \(g\) are changed functions if for every coordinate pair in \(f\), \((a,b)\), there exists a corresponding coordinate pair in the inverse function, \(g\), \((b, a)\). In other words, the coordinate pairs of the inverse functions have the input and output interchanged. Simply one-to-one functions have inverses. Recollect that a one-to-i function has a unique output value for each input value and passes the horizontal line test.
For example, suppose a water runoff collector is built in the shape of a parabolic trough as shown in Effigy \(\PageIndex{2}\). Nosotros tin apply the information in the figure to notice the surface expanse of the water in the trough as a function of the depth of the water.
Considering it will be helpful to have an equation for the parabolic cross-sectional shape, we will impose a coordinate organization at the cross section, with \(ten\) measured horizontally and \(y\) measured vertically, with the origin at the vertex of the parabola (Figure \(\PageIndex{3}\)).
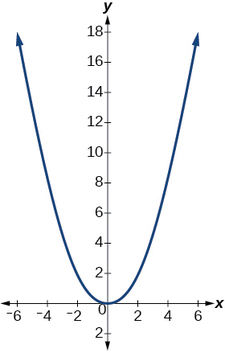
From this nosotros detect an equation for the parabolic shape. We placed the origin at the vertex of the parabola, so nosotros know the equation will have form \(y(10)=ax^ii\). Our equation will demand to pass through the point \((half-dozen, 18)\), from which we can solve for the stretch gene \(a\).
\[ \begin{align*} 18&=a6^two \\[4pt] a &=\dfrac{18}{36} \\[4pt] &=\dfrac{i}{2} \end{align*}\]
Our parabolic cantankerous section has the equation
\(y(x)=\dfrac{i}{two}x^two\)
Nosotros are interested in the surface area of the water, and then we must decide the width at the top of the water every bit a office of the h2o depth. For any depth \(y\), the width will be given by \(2x\), so we demand to solve the equation higher up for \(x\) and find the changed part. Nonetheless, notice that the original role is non one-to-one, and indeed, given whatsoever output there are two inputs that produce the same output, one positive and 1 negative.
To find an inverse, we can restrict our original function to a express domain on which it is one-to-one. In this example, it makes sense to restrict ourselves to positive \(x\) values. On this domain, we can find an inverse by solving for the input variable:
\[ \begin{align*} y&=\dfrac{1}{2}x^2 \\[4pt] 2y&=x^2 \\[4pt] x&=\pm \sqrt{2y} \end{align*}\]
This is not a part as written. We are limiting ourselves to positive \(x\) values, so we eliminate the negative solution, giving us the inverse function we're looking for.
\(y=\dfrac{x^two}{2}\), \(x>0\)
Considering \(x\) is the distance from the center of the parabola to either side, the entire width of the water at the acme will be \(2x\). The trough is 3 feet (36 inches) long, so the surface area will and so exist:
\[ \begin{align*} \text{Expanse} &=l⋅w \\[4pt] &=36⋅2x \\[4pt] &=72x \\[4pt] &=72\sqrt{2y} \end{marshal*}\]
This example illustrates two important points:
- When finding the inverse of a quadratic, we have to limit ourselves to a domain on which the function is one-to-i.
- The inverse of a quadratic role is a square root part. Both are toolkit functions and dissimilar types of ability functions.
Functions involving roots are often chosen radical functions. While it is not possible to observe an inverse of most polynomial functions, some bones polynomials do have inverses. Such functions are called invertible functions, and nosotros use the notation \(f^{−1}(x)\).
Warning: \(f^{−one}(x)\) is not the aforementioned equally the reciprocal of the function \(f(x)\). This use of "–1" is reserved to announce changed functions. To announce the reciprocal of a function \(f(x)\), we would demand to write:
\[ (f(x))^{−1}=\frac{1}{f(x)}.\]
An of import human relationship between inverse functions is that they "undo" each other. If \(f^{−1}\) is the inverse of a role \(f\), then \(f\) is the inverse of the function \(f^{−1}\). In other words, whatsoever the office \(f\) does to \(x\), \(f^{−1}\) undoes it—and vice-versa.
\(f^{−1}(f(x))=10\), for all \(10\) in the domain of \(f\)
and
\(f(f^{−1}(ten))=10\), for all \(x\) in the domain of \(f^{−1}\)
Note that the inverse switches the domain and range of the original function.
VERIFYING Two FUNCTIONS ARE INVERSES OF ONE Another
2 functions, \(f\) and \(k\), are inverses of one another if for all \(x\) in the domain of \(f\) and \(g\),
\(thousand(f(x))=f(grand(x))=10\)
Howto: Given a polynomial function, detect the changed of the office past restricting the domain in such a style that the new function is one-to-1
- Supersede \(f(x)\) with \(y\).
- Interchange \(x\) and \(y\).
- Solve for \(y\), and rename the function \(f^{−1}(x)\).
Case \(\PageIndex{1}\): Verifying Inverse Functions
Bear witness that \(f(x)=\frac{1}{x+i}\) and \(f^{−1}(10)=\frac{1}{x}−ane\) are inverses, for \(x≠0,−1\).
Solution
Nosotros must show that \(f^{−1}(f(x))=x\) and \(f(f^{−1}(x))=10\).
\[ \begin{align*} f^{−1}(f(ten)) &=f^{−1}\left(\dfrac{1}{x+1}\right)\\[4pt] &=\dfrac{1}{\dfrac{1}{ten+1}}−i\\[4pt] &=(ten+1)−1\\[4pt] &=x\cease{align*}\]
and
\[ \begin{align*} f(f^{−1}(x)) &=f(\dfrac{i}{x−1})\\[4pt] &=\dfrac{i}{\left(\dfrac{1}{x−ane}\right)+1}\\[4pt] &=\dfrac{one}{\dfrac{i}{x}}\\[4pt] &=x\end{align*}\]
Therefore, \(f(x)=\dfrac{1}{x+1}\) and \(f^{−1}(x)=\dfrac{ane}{x}−one\) are inverses.
Exercise \(\PageIndex{1}\)
Prove that \(f(ten)=\frac{x+5}{3}\) and \(f^{−ane}(x)=3x−5\) are inverses.
- Answer a
-
\(f^{−i}(f(ten))=f^{−ane}(\frac{10+5}{3})=three(\frac{x+5}{3})−5=(x−v)+5=x\)
- Respond b
-
\(f(f^{−one}(x))=f(3x−5)=\frac{(3x−v)+v}{3}=\frac{3x}{3}=x\)
Example \(\PageIndex{2}\): Finding the Inverse of a Cubic Function
Find the changed of the role \(f(ten)=5x^3+ane\).
Solution
This is a transformation of the basic cubic toolkit role, and based on our noesis of that function, we know it is i-to-one. Solving for the inverse by solving for \(x\).
\(y=5x^3+one\)
\(x=5y^three+1\)
\(x−1=5y^3\)
\(\dfrac{x−1}{5}=y^3\)
\(f^{−1}(10)=\sqrt[iii]{\dfrac{x−1}{5}}\)
Analysis
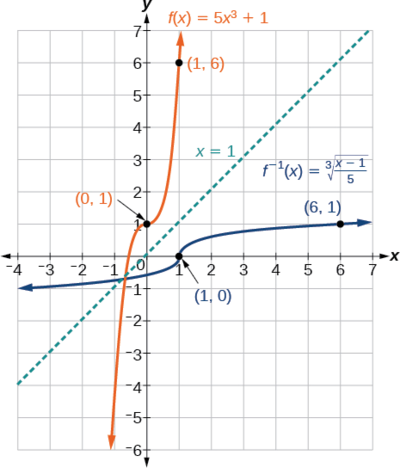
Wait at the graph of \(f\) and \(f^{–ane}\). Find that one graph is the reflection of the other well-nigh the line \(y=ten\). This is always the case when graphing a function and its changed office.
Also, since the method involved interchanging \(ten\) and \(y\), discover corresponding points. If \((a,b)\) is on the graph of \(f\),then \((b,a)\) is on the graph of \(f^{–ane}\). Since \((0,one)\) is on the graph of \(f\), and then \((1,0)\) is on the graph of \(f^{–i}\). Similarly, since \((1,six)\) is on the graph of \(f\),and so \((half dozen,1)\) is on the graph of \(f^{–1}\) (Figure \(\PageIndex{9}\)).
Exercise \(\PageIndex{2}\)
Find the inverse function of \(f(x)=\sqrt[3]{x+4}\).
- Reply
-
\(f^{−1}(x)=x^3−4\)
Restricting the Domain to Detect the Inverse of a Polynomial Part
And so far, we have been able to find the changed functions of cubic functions without having to restrict their domains. Nonetheless, as nosotros know, not all cubic polynomials are one-to-1. Some functions that are non i-to-one may have their domain restricted so that they are one-to-one, only only over that domain. The role over the restricted domain would then take an inverse function. Since quadratic functions are non one-to-one, we must restrict their domain in order to discover their inverses.
RESTRICTING THE DOMAIN
If a function is non one-to-one, it cannot have an inverse. If we restrict the domain of the function and so that it becomes one-to-one, thus creating a new office, this new office will accept an inverse.
How to: Given a polynomial function, restrict the domain of a function that is not one-to-one then find the changed
- Restrict the domain by determining a domain on which the original function is 1-to-i.
- Replace \(f(ten)\) with \(y\).
- Interchange \(x\) and \(y\).
- Solve for \(y\), and rename the function or pair of function \(f^{−i}(x)\).
- Revise the formula for \(f^{−1}(x)\) by ensuring that the outputs of the changed function correspond to the restricted domain of the original function.
Case \(\PageIndex{3}\): Restricting the Domain to Find the Inverse of a Polynomial Role
Observe the inverse function of \(f\):
- \(f(x)={(x−4)}^2\), \(10≥4\)
- \(f(x)={(x−4)}^2\), \(x≤4\)
Solution
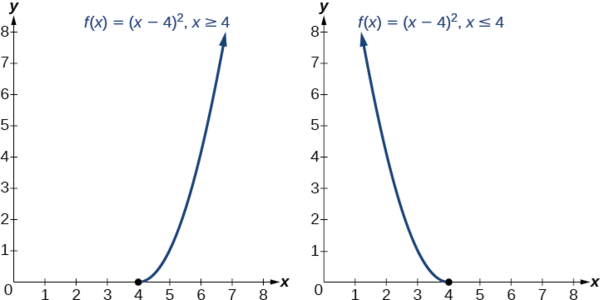
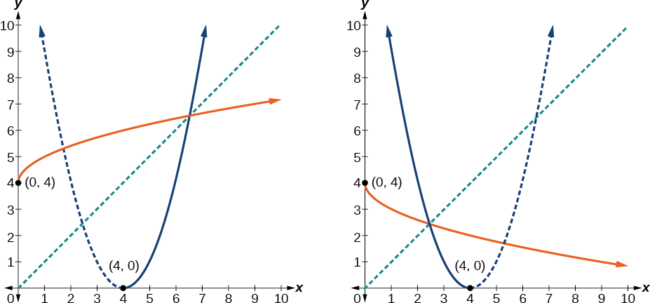
The original part \(f(x)={(x−four)}^2\) is not i-to-one, only the part is restricted to a domain of \(x≥iv\) or \(x≤four\) on which it is one-to-one (Figure \(\PageIndex{half-dozen}\)).
To observe the inverse, start past replacing \(f(x)\) with the simple variable \(y\).
\(y={(x−four)}^2\) Interchange \(x\) and \(y\).
\(ten={(y−iv)}^2\) Take the foursquare root.
\(\pm \sqrt{x}=y−4\) Add together \(four\) to both sides.
\(4\pm \sqrt{10} =y\)
This is non a function as written. Nosotros demand to examine the restrictions on the domain of the original function to determine the inverse. Since we reversed the roles of \(x\) and \(y\) for the original \(f(x)\), we looked at the domain: the values \(x\) could assume. When we reversed the roles of \(x\) and \(y\), this gave us the values \(y\) could assume. For this function, \(x≥iv\), then for the inverse, we should have \(y≥4\), which is what our changed function gives.
- The domain of the original part was restricted to \(x≥iv\), then the outputs of the inverse need to be the same, \(f(x)≥4\), and we must utilize the + case:
\(f^{−1}(x)=4+\sqrt{x}\)
- The domain of the original part was restricted to \(ten≤four\), and then the outputs of the inverse demand to be the aforementioned, \(f(x)≤four\), and we must use the – case:
\(f^{−one}(x)=iv−\sqrt{x}\)
Analysis
On the graphs in Figure \(\PageIndex{6}\), we see the original function graphed on the same set of axes as its changed function. Notice that together the graphs show symmetry almost the line \(y=10\). The coordinate pair \((4,0)\) is on the graph off f and the coordinate pair \((0, 4)\) is on the graph of \(f^{−ane}\). For whatever coordinate pair, if \((a, b)\) is on the graph of \(f\), so \((b, a)\) is on the graph of \(f^{−1}\). Finally, observe that the graph of \(f\) intersects the graph of \(f^{−1}\) on the line \(y=x\). Points of intersection for the graphs of \(f\) and \(f^{−1}\) volition ever lie on the line \(y=x\).
Example \(\PageIndex{four}\): Finding the Inverse of a Quadratic Function When the Restriction Is Non Specified
Restrict the domain and so observe the inverse of
\(f(x)={(x−two)}^2−3\).
Solution
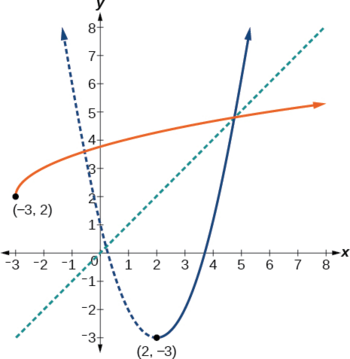
We can see this is a parabola with vertex at \((two,–3)\) that opens upwards. Because the graph will be decreasing on one side of the vertex and increasing on the other side, we can restrict this part to a domain on which it volition exist one-to-one by limiting the domain to \(ten≥2\).
To discover the inverse, we will use the vertex grade of the quadratic. We kickoff by replacing \(f(ten)\) with a uncomplicated variable, \(y\), then solve for \(x\).
\(y={(x−2)}^2−3\) Interchange \(x\) and \(y\).
\(x={(y−two)}^ii−3\) Add 3 to both sides.
\(x+3={(y−2)}^2\) Take the square root.
\(\pm \sqrt{10+3}=y−2\) Add together 2 to both sides.
\(2\pm \sqrt{x+3}=y\) Rename the role.
\(f^{−1}(x)=2\pm \sqrt{x+3}\)
Now nosotros demand to decide which case to employ. Because we restricted our original office to a domain of \(x≥2\), the outputs of the changed should be the same, telling us to utilize the + case
\(f^{−1}(x)=2+\sqrt{10+three}\)
If the quadratic had not been given in vertex form, rewriting information technology into vertex grade would be the commencement step. This fashion we may easily observe the coordinates of the vertex to help us restrict the domain.
Analysis
Detect that nosotros arbitrarily decided to restrict the domain on \(x≥2\). We could just as easily take opted to restrict the domain to \(x≤two\), in which case \(f^{−1}(ten)=2−\sqrt{x+3}\). Observe the original function graphed on the same set up of axes as its inverse function in Figure \(\PageIndex{7}\). Notice that both graphs testify symmetry about the line \(y=10\). The coordinate pair \((2, −3)\) is on the graph of \(f\) and the coordinate pair \((−3, 2)\) is on the graph of \(f^{−1}\). Observe from the graph of both functions on the aforementioned gear up of axes that
domain of \(f=\) range of \(f^{–1}=[two,\infty)\)
and
domain of \(f^{–i}=\) range of \(f=[–three,\infty)\).
Finally, observe that the graph of \(f\) intersects the graph of \(f^{−1}\) along the line \(y=x\).
Exercise \(\PageIndex{4}\)
Observe the changed of the function \(f(x)=x^2+one\), on the domain \(x≥0\).
- Answer
-
\(f^{−1}(x)=\sqrt{ten−1}\)
Finding Inverses
Notice that the functions from previous examples were all polynomials, and their inverses were radical functions. If we desire to find the inverse of a radical function, we will need to restrict the domain of the reply because the range of the original role is express.
How to: Given a radical function, detect the inverse
- Determine the range of the original function.
- Replace \(f(x)\) with \(y\), then solve for \(x\).
- If necessary, restrict the domain of the changed function to the range of the original function.
Case \(\PageIndex{5}\): Finding the Inverse of a Radical Function
Restrict the domain of the function \(f(x)=\sqrt{x−4}\) and then notice the inverse.
Solution
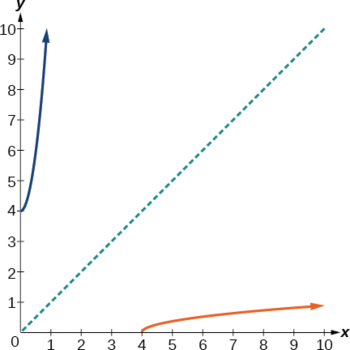
Notation that the original office has range \(f(x)≥0\). Replace \(f(x)\) with \(y\), then solve for \(10\).
\(y=\sqrt{x−iv}\) Replace \(f(ten)\) with \(y\).
\(x=\sqrt{y−4}\) Interchange \(x\) and \(y\).
\(x=\sqrt{y−four}\) Square each side.
\(10^2=y−4\) Add 4.
\(x^two+4=y\) Rename the function \(f^{−1}(ten)\).
\(f^{−i}(x)=x^2+iv\)
Call up that the domain of this function must be limited to the range of the original function.
\(f^{−1}(x)=10^2+4\), \(10≥0\)
Analysis
Notice in Effigy \(\PageIndex{8}\) that the inverse is a reflection of the original function over the line \(y=x\). Because the original function has only positive outputs, the changed function has only nonnegative inputs.
Practice \(\PageIndex{5}\)
Restrict the domain and then observe the inverse of the office \(f(10)=\sqrt{2x+3}\).
- Answer
-
\(f^{−one}(x)=\frac{x^2−3}{two}\), \(ten≥0\)
Solving Applications of Radical Functions
Radical functions are common in physical models, equally we saw in the section opener. Nosotros now have enough tools to be able to solve the problem posed at the showtime of the section.
Case \(\PageIndex{half dozen}\): Solving an Application with a Cubic Office
A mound of gravel is in the shape of a cone with the height equal to twice the radius. The volume of the cone in terms of the radius is given by
\[V=\dfrac{two}{3}\pi r^3 \nonumber\]
Find the changed of the function \(Five=\frac{2}{3}\pi r^3\) that determines the volume \(Five\) of a cone and is a function of the radius \(r\). Then use the inverse role to calculate the radius of such a mound of gravel measuring 100 cubic feet. Use \(\pi=3.xiv\).
Solution
Start with the given function for \(V\). Notice that the meaningful domain for the function is \(r>0\) since negative radii would not make sense in this context nor would a radius of \(0\). Also note the range of the function (hence, the domain of the changed office) is \(V>0\). Solve for \(r\) in terms of \(5\), using the method outlined previously. Note that in real-world applications, nosotros practise not swap the variables when finding inverses. Instead, we change which variable is considered to exist the independent variable.
\[ Five =\dfrac{2}{iii}\pi r^three\nonumber \]
Solve for \(r^3\).
\[r^3 =\dfrac{3V}{2\pi} \nonumber\]
Solve for \(r\).
\[ r=\sqrt[iii]{\dfrac{3V}{2\pi}} \nonumber \]
This is the event stated in the department opener. Now evaluate this for \(V=100\) and \(\pi=3.xiv\).
\[ \begin{align*} r&=\sqrt[three]{\dfrac{3V}{2\pi}} \\[4pt] &=\sqrt[three]{\dfrac{3⋅100}{2⋅3.fourteen}} \\[4pt] &≈\sqrt[3]{47.7707} \\[4pt] &≈3.63 \terminate{align*}\]
Therefore, the radius is most 3.63 ft.
Determining the Domain of a Radical Part Composed with Other Functions
When radical functions are composed with other functions, determining domain tin can become more complicated.
Instance \(\PageIndex{vii}\): Finding the Domain of a Radical Function Composed with a Rational Function
Detect the domain of the function:
\[f(x)=\sqrt{\frac{(ten+two)(x−3)}{(x−1)}}. \nonumber\]
Solution
Because a foursquare root is only defined when the quantity under the radical is not-negative, nosotros need to make up one's mind where
\[\frac{(x+2)(ten−3)}{(x−1)}≥0. \nonumber\]
The output of a rational function tin can alter signs (change from positive to negative or vice versa) at ten-intercepts and at vertical asymptotes. For this equation, the graph could change signs at \(x=–two\), \(i\), and \(iii\).
To determine the intervals on which the rational expression is positive, we could test some values in the expression or sketch a graph. While both approaches work every bit well, for this instance we will use a graph as shown in Figure \(\PageIndex{ix}\).
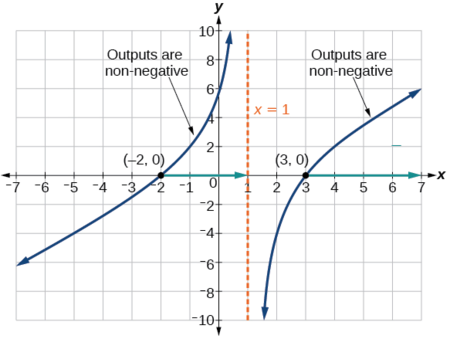
This part has two x-intercepts, both of which exhibit linear beliefs most the x-intercepts. In that location is one vertical asymptote, respective to a linear factor; this behavior is like to the basic reciprocal toolkit function, and there is no horizontal asymptote considering the degree of the numerator is larger than the degree of the denominator. At that place is a y-intercept at \((0,\sqrt{6})\).
From the y-intercept and x-intercept at \(ten=−2\), nosotros tin sketch the left side of the graph. From the behavior at the asymptote, nosotros can sketch the right side of the graph.
From the graph, we can now tell on which intervals the outputs volition be non-negative, so that we can exist sure that the original function \(f(x)\) will be defined. \(f(x)\) has domain \(−2≤x<1\) or \(x≥iii\), or in interval notation, \([−2,1)∪[3,\infty)\).
Finding Inverses of Rational Functions
As with finding inverses of quadratic functions, it is sometimes desirable to notice the inverse of a rational function, particularly of rational functions that are the ratio of linear functions, such every bit in concentration applications.
Example \(\PageIndex{8}\): Finding the Inverse of a Rational Role
The role
\[\displaystyle C=\frac{twenty+0.4n}{100+n}\]
represents the concentration \(C\) of an acid solution after \(n\) mL of 40% solution has been added to 100 mL of a 20% solution. Kickoff, observe the inverse of the office; that is, find an expression for \(north\) in terms of \(C\). And then use your result to determine how much of the 40% solution should be added and so that the terminal mixture is a 35% solution.
Solution
We first want the inverse of the role in order to determine how many mL we need for a given concentration. Nosotros will solve for \(n\) in terms of \(C\).
\[ \begin{align*} C&=\dfrac{20+0.4n}{100+northward} \\[4pt] C(100+north)&=xx+0.4n\\[4pt] 100C+Cn&=20+0.4n\\[4pt] 100C−20&=0.4n−Cn\\[4pt] 100C−20&=(0.iv−C)n\\[4pt] n&=\dfrac{100C−20}{0.4−C}\end{align*}\]
Now evaluate this role at 35%, which is \(C=0.35\).
\[ \begin{marshal*} north&=\dfrac{100(0.35)−xx}{0.4−0.35}\\[4pt] &=\dfrac{15}{0.05}\\[4pt] &=300\end{align*}\]
We can conclude that 300 mL of the xl% solution should be added.
Practice \(\PageIndex{8}\)
Find the inverse of the function \(f(x)=\frac{x+iii}{x−2}\).
- Answer
-
\(f^{−i}(x)=\frac{2x+3}{x−1}\)
Primal Concepts
- The inverse of a quadratic function is a square root function.
- If \(f^{−ane}\) is the changed of a function \(f\), then \(f\) is the changed of the part \(f^{−ane}\). See Instance \(\PageIndex{i}\).
- While it is not possible to find an inverse of near polynomial functions, some basic polynomials are invertible. Come across Instance \(\PageIndex{2}\).
- To detect the inverse of certain functions, we must restrict the role to a domain on which information technology will be 1-to-i. See Examples \(\PageIndex{iii}\) and \(\PageIndex{four}\)
- When finding the inverse of a radical function, nosotros need a restriction on the domain of the reply. See Example \(\PageIndex{5}\) and \(\PageIndex{7}\).
- Inverse and radical and functions tin can exist used to solve application problems. Run across Examples \(\PageIndex{half dozen}\) and \(\PageIndex{8}\).
Source: https://math.libretexts.org/Bookshelves/Precalculus/Book:_Precalculus_%28OpenStax%29/03:_Polynomial_and_Rational_Functions/3.08:_Inverses_and_Radical_Functions
Posted by: jonesaffeekly.blogspot.com



0 Response to "How To Find Inverse Of A Square Root Function"
Post a Comment